آزمون کلموگروف-اسمیرنوف برای نرمال بودن در spss
یک آزمون جایگزین برای بررسی نرمال بودن ،شاپیرو ویلک است.
- آزمون کلموگروف اسمیرنوف برای نرمال بودن چیست؟
- آزمون کلموگروف-اسمیرنوف درspss از روش NPAR TESTS
- آزمون کلموگروف-اسمیرنوف درspssبا استفاده از EXAMINE VARIABLES
- گزارش آزمون کلموگروف اسمیرنوف
- نتایج غلط در SPSS؟
بررسی نرمال بودن با آزمون کلموگروف اسمیرنوف چیست؟
ازمون کلموگروف_اسمیرنوف بررسی میکند که ایا نمره ها درجامعه از توزیعی تبعیت میکنند.برای جلوگیری از سردرگمی، 2 ازمون کلموگروف_اسمیرنوف وجود دارد:
- آزمون کلموگروف اسمیرنوف تک نمونه ای برای آزمودن اینکه، متغیر از توزیع معین داده شده در یک جامعه پیروی می کند یا خیر. “توزیع داده شده” معمولا_نه همیشه_توزیع نرمال است. از این جهت” ازمون کلموگروف_اسمیرنوف برای نرمال بودن”گوییم.
- همچنین آزمون کلموگروف _اسمیرنوف برای نمونه های مستقل برای آزمودن این است که یک متغیر توزیع یکسان در 2 جامعه دارد یا خیر.
از نظر تئوری، برای آزمون کلموگروف اسمیرنوف می توان به هر دو آزمون رجوع کرد(اما معمولاً به آزمون کلموگروف اسمیرنوف تک نمونه ای اشاره دارد) و بهتر است از آن اجتناب شود. ضمناً، هر دو آزمون کلموگروف اسمیرنوف در SPSS وجود دارد.
آزمون کلموگروف اسمیرنوف_مثالی ساده
من جامعه 1،000،000 نفری دارم. فکر می کنم زمان واکنش آنها در بعضی کارها به طور نرمال توزیع شده است. 233 نفر از این افراد را نمونه گیری کرده و زمان واکنش آنها را اندازه گیری می کنم. اکنون توزیع فراوانی مشاهده شده از این نمونه احتمالاً کمی _نه خیلی زیاد_ متفاوت از توزیع نرمال خواهد بود. در این حال، یک هیستوگرام از زمان واکنش مشاهده شده رسم می کنم و یک توزیع نرمال را با همان میانگین و انحراف استاندارد بر روی هم می گذارم. نتیجه در پایین نشان داده شده است.

توزیع فراوانی نمرات کاملاً با منحنی نرمال همخوانی ندارد. اکنون، می توانم درصد مواردی را که از منحنی نرمال _درصد مناطق قرمز در نمودار _خارج می شوند، محاسبه کنم. این درصد آماره آزمون است :که در یک عدد بیان می کند داده های من با فرضیه صفر چقدر تفاوت دارد. بنابراین این عدد نشان می دهد که نمرات مشاهده شده تا چه اندازه از توزیع نرمال منحرف می شوند.
حال، اگر فرضیه صفر من درست باشد، این درصد انحراف احتمالاً بسیار کم می باشد. یعنی این انحراف کوچک دارای احتمال یا p-value زیاد است.
برعکس، یک درصد انحراف بزرگ بسیار بعید است و نشان می دهد که زمان واکنش مشاهدات توزیع نرمال در کل جامعه ندارد. بنابراین یک انحراف بزرگ p-value کوچکی دارد. به عنوان یک قاعده کلی، اگر p < 0.05 انگاه فرضیه صفر را رد میکنیم .پس اگر p < 0.05، معتقدیم متغیر مورد نظر ما در جامعه از توزیع نرمال تبعیت نمیکند.
آزمون کلموگروف اسمیرنوف_آماره آزمون
این ساده ترین راه برای درک چگونگی عملکرد آزمون کلموگروف اسمیرنوف است.
از لحاظ محاسباتی، هرچند، عملکرد متفاوتی دارد: فراوانی های نسبی تجمعی مشاهده شده را در مقابل مورد انتظار همانطور که در زیر نشان داده شده است، مقایسه میکند.

آزمون کلموگروف اسمیرنوف از قدر مطلق حداکثر اختلاف بین این منحنی ها با D به عنوان آماره آزمون خود استفاده می کند. در این نمودار، قدر مطلق حداکثر اختلاف D، (0.48 0.41 =) 0.07 است و در زمان واکنش 960 میلی ثانیه رخ می دهد.به خاطر داشته باشید که 07/0 = D عددی است که در یک دقیقه در خروجی SPSS با ان مواجه خواهیم شد.
آزمون کلموگروف اسمیرنوف در SPSS
دو روش برای اجرای آزمون در SPSS وجود دارد.
- NPAR TESTSکه از مسیر Nonparametric Test -> Legacy Dialogs-> Sample K-S… یافت میشود، روش انتخاب ماست زیرا خروجی دقیق و جزئی ایجاد می کند.
- EXAMINE VARIABLES از مسیر Analyze Descriptive Statistics Explore
این دستور هم آزمون کلموگروف اسمیرنوف و هم آزمون شاپیرو ویلک را اجرا می کند.
توجه داشته باشید که EXAMINE VARIABLES به طور پیش فرض مقادیر گمشده را از لیست حذف میکند. بنابراین اگر 5 متغیر را آزمون کنم،دراین 5 آزمون فقط از نمونه هایی استفاده می کند که درهیچ یک از این 5 متغیر مقدار گمشده نباشد. معمولاً این، آن چیزی نیست که می خواهید اما نشان خواهیم داد که چگونه از این امر جلوگیری کنید.
ما هر دو روش را تماما با استفاده از speedtasks.sav نشان خواهیم داد، که بخشی از آن در زیر نشان داده شده است.

سوال اصلی تحقیق ما این است که کدام یک از متغیرهای زمان واکنش به طور نرمال در جامعه توزیع می شود؟ این داده ها مثالی از کتاب درسی است که چرا باید قبل از شروع ویرایش یا تجزیه و تحلیل، داده های خود را کاملاً بررسی کنید. بیایید فقط برخی از هیستوگرام ها را از syntax زیر اجرا کنیم.
اگرتوزیع ها قابل قبول به نظر رسیدند، هیستوگرام های اساسی را برای بازرسی اجرا کنید.
frequencies r01 to r05
/format notable
/histogram normal.
توجه داشته باشید که برخی توزیع ها به هیچ وجه قابل قبول به نظر نمی رسند.
نتایج

توجه داشته باشید که برخی توزیع ها به هیچ وجه قابل قبول به نظر نمی رسند. اما کدام یک احتمالاً به طور نرمال توزیع شده اند؟
آزمون کلموگروف _اسمیرنوف از NPAR TEST
مسیرمورد نظر ما برای اجرای آزمون کلموگروف اسمیرنوف
Analyze Nonparametric Tests Legacy Dialogs 1-Sample K-S.
است که درزیر نمایش داده شده است.

سپس، ما فقط همانطور که در زیر نشان داده شده گفتگو را پر می کنیم.

با کلیک روی Paste ، نتیجه درsyntaxزیر نمایش داده شده است. بیایید آن را اجرا کنیم.
Syntax ازمون کلموگروف_اسمیرنوف از ازمون های ناپارارمتری
مسیر ازمون کلموگروف_اسمیرنوف تک نمونه ای
analyze – nonparametric tests – legacy dialogs – 1 sample ks-test
NPAR TESTS
/K-S(NORMAL)=r01 r02 r03 r04 r05
/MISSING ANALYSIS.
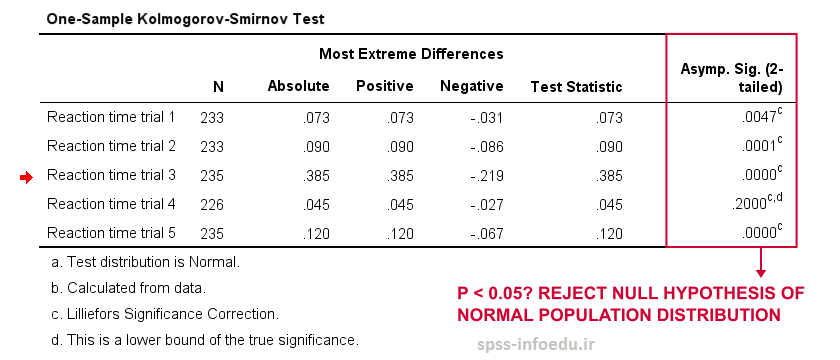
فقط زمان واکنش 4 دارای p > 0.05 است و بنابراین به نظر می رسد به طور نرمال در جامعه توزیع شده است.
نتایج

اول از همه، توجه داشته باشید که آماره آزمون برای اولین متغیر 0.073 است، درست همانطور که در نمودار فراوانی های نسبی تجمعی کمی جلوتر مشاهده کردیم. نمودار دقیقاً همان داده هایی راکه مورد آزمون قرار دادیم،نگه میدارد بنابراین این نتایج به خوبی همسو می شوند.
در مورد سوال تحقیق: به نظر می رسد زمان های واکنش فقط برای آزمایش 4 به طور نرمال توزیع شده است.
ازمون کلموگروف_اسمیرنوف در spss از EXAMINE VARIABLES
یک روش جایگزین برای اجرای آزمون کلموگروف اسمیرنوف از
from Analyze Descriptive Statistics Explore
همانطور که در زیر نشان داده شده است اغاز میشود.


Syntax ازمون کلموگروف اسمیرنوف از ازمون های غیر پارامتری
مسیر ازمون کلموگروف اسمیرنوف تک نمونه ای
*One-sample Kolmogorov-Smirnov test from analyze – descriptive statistics
EXAMINE VARIABLES=r01 r02 r03 r04 r05
/PLOT BOXPLOT NPPLOT
/COMPARE GROUPS
/STATISTICS NONE
/CINTERVAL 95
/MISSING PAIRWISE /*IMPORTANT!*/
/NOTOTAL
نسخه کوتاه تر
EXAMINE VARIABLES r01 r02 r03 r04 r05
/PLOT NPPLOT
/missing pairwise /*IMPORTANT!*/.
نتایج

به عنوان یک قاعده کلی، نتیجه می گیریم که اگر“Sig.” < 0.05 انگاه متغییر موردنظر به صورت نرمال توزیع نشده است.
بنابراین نتایج درهردو آزمون کلموگروف_اسمیرنوف و شاپیروویلک نشان می دهد که فقط زمان واکنش آزمایش 4 از توزیع نرمال در کل جامعه تبعیت میکند.
علاوه بر این، توجه داشته باشید که نتایج آزمون کلموگروف_اسمیروف با نتایج بدست آمده از NPAR TESTS یکسان است
گزارش آزمون کلموگروف_اسمیرنوف
برای گزارش نتایج آزمون خود به دنبال رهنمودهای APA هستیم، ما چیزی مانند “یک آزمون کلموگروف اسمیرنوف نشان می دهد که زمان های واکنش در آزمایش 1 از توزیع نرمال پیروی نمی کند، D (233) = 0.07، p = 0.005.” می نویسیم. برای متغیرهای اضافی، سعی کنید این را کوتاه کنید اما مطمئن شوید که آن را اضافه کنید
- D(برای “تفاضل ها”)،اماره ازمون کلموگروف _اسمیرنوف
- Df درجه ازادی(برابر با N)
- P معنی داری آماری

نتایج غلط در SPSS؟
اگر دانشجویی هستید که فقط می خواهد در یک آزمون قبول شوید، اکنون می توانید مطالعه را متوقف کنید. فقط مراحلی را که تا اینجا گفتیم دنبال کنید و خوب خواهید شد.
خوب، حالا بیایید دقیقاً همان آزمایشات را دوباره در SPSS نسخه 18 اجرا کنیم و نگاهی به خروجی بیندازیم.

در این خروجی، مقادیر دقیق p-values گنجانده شده است و _خوشبختانه_ به مقادیر p-values مجانبی بسیار نزدیک هستند. متاسفانه، نتایج نسخه 18 SPSS بسیار متفاوت از نسخه 24 SPSS که تاکنون گزارش داده ایم.
به نظر می رسد دلیل آن این است که که تصحیح معنی داری لی لی فورس در نسخه های جدید SPSS اعمال می شود. به نظر می رسد در نتیجه سطح معنی داری مجانبی با معنی داری دقیق تفاوت بیشتری نسبت به وقتی که تصحیح ضمنی ندارد، نشان می دهد. این باعث ایجاد تردیدهای جدی در مورد درستی “نتایج لی لی فورس” _به طور پیش فرض در نسخه های جدید SPSS _می شود
شواهد همسویی برای این پیشنهاد توسط همکار من Alwin Stegeman که تمام آزمایشات را در Matlab انجام داد، جمع آوری شد. نتایج Matlab با نتایج SPSS 18 سازش دارد و از_ این رو_ با نتایج جدیدترسازگار نیست.

آزمون نرمال بودن کلموگروف اسمیرنوف _کارایی محدود
آزمون کلموگروف_اسمیرنوف اغلب برای آزمودن فرض نرمال مورد نیاز بسیاری از آزمونهای آماری مانند ANOVA، آزمون t و بسیاری دیگر است. با این حال، اگر اندازه های نمونه مناسب باشد، مثلا N ≥ 25، تقریباً به طور معمول نادیده گرفته می شود چراکه چنین آزمایشاتی در برابر نقیض این فرض قوی هستند. * بنابراین، آزمون های نرمال بودن فقط برای اندازه نمونه کوچک مورد نیاز است اگر هدف این است که فرض نرمال بودن را برآورده کنیم.
متأسفانه، اندازه های کوچک نمونه منجر به توان آماری کم برای آزمون های نرمال می شود. این بدان معناست که انحرافات اساسی از حالت نرمال در معنی داری آماری(sig )اعمال نمیشود. این آزمایش می گوید هیچ انحرافی از حالت نرمال وجود ندارد در حالی که در واقع بسیار زیاد است. به طور خلاصه، وضعیتی که در آن به آزمایش های نرمال نیازاست _اندازه های کوچک نمونه_ ، وضعیتی است که در آن عملکرد ضعیف دارند.
