
یک بیمارستان می خواهد بداند که داروی homeopathic برای افسردگی در مقایسه با درمان های دیگر چگونه عمل می کند. آنها 4 دارو را برای 100 بیمار به مدت 2 هفته تجویز و سپس سطح افسردگی آنها را اندازه گیری کردند. بخشی از داده های این آزمایش در بالا نشان داده شده است.
بازبینی داده ها-نمودار هیستوگرام
قبل از اجرای هرگونه آزمون آماری، همیشه اطمینان حاصل کنید که داده های شما در وهله اول در محدوده صحیح و متعارف هستند. نمودار هیستوگرام دسته بندی شده اساسا همه اطلاعات را در یک قاب واحد بیان می کند. بسیاری از کاربران spss چنین نمودارهایی را اجرا نمی کنند اما استفاده از این نمودار ها بسیار مفیر است. تصاویر زیر نحوه اجرای آن را نشان می دهد.
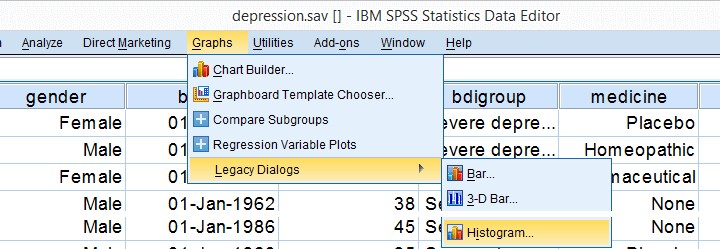
در مرحله3 می توانید برای نمودار خود عنوان اضافه کنید. ما برای نمودارهای خود عنوان “توزیع BDI در هر دارو” را انتخاب کردیم .

دستور نمودار هیستوگرام ها
با کلیک روی دکمه Paste، دستورزیررامشاهده می کنید.
اجرای این دستور نمودار را نمایش می دهد .
*Run histograms of BDI scores for the four medicines separately.
GRAPH
/HISTOGRAM=bdi
/PANEL ROWVAR=medicine ROWOP=CROSS
/TITLE=’Distribution BDI per Medicine’.
نتیجه

این نمودارهای ساده اطلاعات زیادی در مورد داده های ما دارند. نکات مهم عبارتند از:
- همه توزیع ها قابل قبول به نظر می رسند. مقادیر BDI خیلی کم یا خیلی زیاد نمی بینیم پس باید به عنوان مقادیر گمشده کاربر تنظیم شوند و به نظرمی رسدنمرات BDI دارای توزیع نرمال هستند.
- “None” بالاترین امتیاز BDI را دارد که نشان دهنده بدترین علایم افسردگی است. “Pharmaceutical” منجر به کمترین علایم بیماری افسردگی می شود و دو درمان دیگر در این بین قرار دارند.
- چهار هیستوگرام تقریباً به یک اندازه گسترده هستند ، که نشان می دهد واریانس مقادیر BDI هرچهار دارو تقریباً باهم برابر است.
جدول میانگین
اکنون با استفاده ازجدول میانگین نگاه دقیق تری به داده ها می اندازیم. ما می توانیم این کار را از طریق
Analyz >>> Compare >>> Means
انجام دهیم این دستور بسیار ساده است فقط باید آن را به سرعت تایپ کنید.
*Run basic means table.
means bdi by medicine
/cells count min max mean variance.
*Note: use /cells to choose which columns you’d like in which order.
نتیجه

تعجب آور نیست که جدول ما بیشتر آنچه را که قبلاً در نمودارهیستوگرام دیده بودیم نشان میدهد. توجه داشته باشید در(ستون “N”) هر دارو 25 مشاهده دارد بنابراین این چهارمتغیر مقادیرگمشده ندارند .
بنابراین ایا می توان نتیجه گرفت که “Pharmaceutical” بهترین عملکرد و “None” بدترین عملکرد را دارد؟
مااین ازمایش را می توانیم روی نمونه انجام دهیم ولی برای جامعه (همه افرادی که از افسردگی رنج می برند) نمی توانیم این ازمایش را انجام دهیم. مشکل اساسی در اینجا این است که نمونه ها با جامعه هایی که از آن گرفته می شوند متفاوت است. اگر چهار دارو در جامعه ماعملکرد یکسانی داشته باشند ، ولی ممکن تفاوت های کمی بین میانگین نمونه هایمان مشاهده کنیم. با این حال ، اگر همه داروها به طور مساوی در جامعه ما عمل کنند ، اختلافات زیادی در نمونه وجود ندارد. توضیح در مورد این استدلال را، در ANOVA – What Is It? مطالعه کنید.
سوالی که اکنون به آن پاسخ خواهیم داد این است: آیا میانگین نمونه به اندازه کافی متفاوت است تا فرضیه صفر را که میانگین مقادیر BDI در جامعه برابر است را ردکند؟
آزمون همه کاره و آزمونهای تعقیبی ANOVA
معمولاًANOVA را در 2 مرحله اجرا می کنیم:
- ابتدا آزمایش می کنیم که آیا همه میانگین ها باهم برابر اند. این را اغلب
ازمون همه کاره می نامند. ” Omnibus “که درلاتین به معنای “درمورد همه چیز” است.
- اگر نتیجه بگیریم که همه میانگین ها برابر نیستند ، گاهی اوقات آزمون می کنیم که دقیقاً کدام میانگین ها برابر نیستند. این شامل آزمون های تعقیبی است. “Post hoc” در لاتین به معنای “پس از آن” است که ” آن” به آزمون همه کاره اشاره دارد.
این روش استاندارد نشان می دهد درصورت انجام آزمون همه کاره ، باید آزمونهای تعقیبی را هم انجام دهیم
این”از نظر آماری قابل توجه است”. بااین حال، می توان ادعا کرد شما همیشه باید آزمونهای تعقیبی را انجام دهید. مثلادر برخی از زمینه ها مانند تحقیقات بازار ، این بسیار رایج است. برعکس هم می توانید استدلال کنید که هرگز نباید از آزمونهای تعقیبی استفاده کنید زیرا آزمون همه کاره کفایت می کند: برخی از تحلیلگران ادعا می کنند که اجرای آزمونهای تعقیبی، تجزیه و تحلیل بیش از حد داده ها است. بسیاری از دانشمندان علوم اجتماعی متوجه اهمیت امارنمی شوند – زیرا آنها نمیفهمند دقیقامیانگین چیست – و از موارد جالبترهم مانند:اندازه اثر و فواصل اطمینان غافل می شوند.
در هر صورت ، آزمون های تعقیبی با اجرای ازمون های همه کاره بهتر روشن می شود. اما قبل از انجام این کار ، بیایید نگاهی سریع به مفروضات مورد نیاز برای اجرای ANOVA بیندازیم.
مفروضات ANOVA
ANOVA در SPSS خوب عمل میکند اما درصورتی می توانیم نتایج را جدی بگیریم که داده ها 3 فرض را داشته باشد :
- مشاهدات مستقل (هرردیفcells درSPSS) نشان دهنده یک شخص منحصر به فرد یا یک واحد آماری است. یعنی ما معمولاً بیش از یک ردیف داده برای یک نفر نمی خواهیم.
- متغیرهادارای توزیع نرمال در جامعه بنظر می رسند اگر به هیستوگرام هایی که قبلاً بازرسی کردیم نگاه کنیم . علاوه بر این ، براساس قضیه حد مرکزی ،باتوجه به حجم زیاد نمونه هافرض نرمال بودن داده ها نقض نمی شود .
- همگنی به این معنی است که واریانس BDI جامعه در همه گروه های دارویی باهم برابر است و تقریباً در واریانس های برابرنمونه منعکس شده است. نمودار هیستوگرام به ما نشان می دهد که این مورد وجود دارد ، اما ما با استفاده از آزمون لوین هنگام اجرای ANOVA سعی در تأیید آن داریم.
اجرای ANOVA در SPSS

روشهای زیادی برای اجرای ANOVA در SPSS وجود دارد. امروزه ، ما به دنبال یک مدل خطی عمومی هستیم که خروجی را دقیق بیان کند.
قبل ازاجرای دستورها ، به طور خلاصه وارد Post Hoc و Options می شویم

آزمون تعقیبی راباتوکی HSD(HSDمخفف “تفاوت صادقانه قابل توجه”است) اجرامی کنیم ، که با”Tukey “نمایش داده شده است. وقتی در مورد خروجی توضیح بدیم نحوه کاررا هم میگوییم .

“برآورد اندازه اثر” به صورت مجذوروجزئی وجود دارد. “آزمون همگنی” شامل آزمون لوین برای واریانس های برابر در خروجی است.
دستورآزمون تعقیبی ANOVA در SPSS
باتوجه به عکس های قبلی دستورات را به ترتیب می نویسیم، اجرا می کنیم و خروجی را توضیح می دهیم.
*ANOVA syntax with Post Hoc (Tukey) test, homogeneity (Levene’s test) and effect size (partial eta squared).
UNIANOVA bdi BY medicine
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/POSTHOC=medicine(TUKEY)
/PRINT=ETASQ HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=medicine.
خروجی آزمون لوین ANOVA در SPSS

ازمون لوین بررسی می کند که آیا واریانس جامعه BDI برای همه چهار گروه دارویی برابر است یا خیر ، این برای ANOVA مورد نیاز است. به عنوان یک قاعده کلی ، ما فرضیه صفر را رد می کنیم اگر 0.05>(“Sig “یا)p . درمثال ما ، 0.949 = p بنابراین فرضیه صفر واریانس های برابر (یا همگنی) را رد نمی کنیم. ما فرض می کنیم که واریانس همه جامعه هابرابر است بنابراین این فرض ANOVA با داده های ما مطابقت دارد.
خروجی اثرات بین گروهی ANOVA درSPSS
در جدول زیر ، آزمون همه کاره ANOVA گزارش شده است.

1 فرضیه صفر ما این است که میانگین جامعه برای همه داروهای تجویز شده برابر است. =0.000(“sig”) P این از 0.05کمتراست-بنابراین ما این فرضیه را رد می کنیم:
میانگین همه جامعه هابرابر نیستند. برخی از داروها در مقایسه با سایر داروها میانگین مقدار BDI کمتری دارند.
2داروهای مختلف تجویز شده حدود 39٪ از واریانس مقادیر BDI را تشکیل می دهند. این اندازه اثر است که به صورت مجذوروجزئی نشان داده شده است.
مربع جزئی اتا 3مجموع مربعات دارویی است که بر 5مجموع مربع های تصحیح شده تقسیم می شود (0.39=7071/2780).
4مجموع توان دوم های خطا ،واریانس مقادیر BDI است که برای داروها محاسبه نشده است رانشان دهنده. توجه داشته باشید که 3+ 4 = 5 .
خروجی مقایسه های چندگانه ANOVAدر SPSS
تاکنون به این نتیجه رسیدیم که بعیداست که میانگین چهار جامعه باهم برابرباشند. دقیقاً کدام میانگین هاباهم تفاوت دارند؟ خوب ، هیستوگرام ها و جداول میانگین هایی که قبل از ANOVA اجرا کردیم ،جواب درست رابه مانشان می دهد. حال می خواهیم نتایج رابایک ازمون رسمی تر نشان دهیم: توکیHSD در جدول مقایسه های چندگانه نشان داده شده است.

اکنون نتایج 4میانگین را که در 6سطرمجزا(6=0.5 x4 x ((4-1)) آمده است مقایسه می کنیم ،هرکدام از آنها دو بار در جدول ذکر شده است. سه روش برای بیان میانگین هایی که ممکن است متفاوت باشند وجود دارد:
1 اختلافات میانگین معنی دار آماری با ستاره (*) نشان داده می شود. به عنوان مثال ، خط اول به ما می گوید که میانگین BDI “None”بامقدار6.7 امتیاز بالاتری از Placebo دارد – در واقع این اختلاف بسیار زیاد است ، زیرا نمرات BDI می تواندبین 0 تا 63 باشد.
2به عنوان یک قاعده کلی ، 05/0> “sig”اختلاف آماری معنی داری را بین دو میانگین نشان می دهد.
3فاصله اطمینان میانگین صفرنمی شودچون اختلاف صفربین میانگین های جامعه بعید است .
بدیهی است نتایج 1 ، 2 و 3 نتایج مشابهی هستند.
گزارش ازمون های تعقیبی ANOVA ، APA در SPSS
ANOVA را با آزمونهای تعقیبی اجرا وتفسیر میکنیم. جداول ایجاد شده به استانداردهای APA نزدیک نیستند. ما می توانیم جدول بسیار بهتری بادستور CTABLES در زیر اجرا کنیم. راستش ، من مطمئن نیستم که چگونه می توان آن را از فهرست ایجاد کرد ، اما امیدوارم پس از جایگزینی 2 نام متغیر ، بتوانید دوباره از آن استفاده کنید.
دستورSPSS ،CTABLES برای جدول APA ANOV
*APA ANOVA table – means, SD’s and Bonferroni corrected pairwise t-tests.
ctables
/table bdi [s] [count ‘n’ f3 mean ‘Mean’ f3.2 stddev ‘SD’ f3.2] by medicine [c]
/categories variables = medicine total = yes position = after
/slabels position = row
/titles title = ‘Table 1 – Mean BDI Scores per Medicine with Bonferroni Adjusted Pairwise T-Tests’
/comparetest type = mean style = simple merge = yes.
*Note: running this requires SPSS custom tables license.
نتیجه

حروف بزرگ در این جدول (A ، B و…) نشان می دهد کدام میانگین هاباهم تفاوت دارد. SPSS همچنین انحرافات استاندارد وحجم نمونه را علامت گذاری می کند. این اشتباه است زیرا اینها مقایسه نمی شوند. آنها همیشه علامت یکسانی دارند برای میانگین . بنابراین دراینجاهمه چیز را نادیده بگیرید ، به جز میانگین را.
شناخت این جدول با دقیق خواندن پاورقی های آن آغاز می شود.اول ازهمه “آزمون های دو طرفه” به نمونه های مستقل آزمون تی با استفاده از اهمیت 2 دم اشاره دارد. بعدازآن ، هر تفاوت معنی دار آماری فقط یک بار در این جدول نشان داده شده است. همانطور که قبلاً نشان داده شد ، 4 میانگین 6 جفت میانگین منحصر به فرد را ارائه می دهد. در مجموع ، این جدول دارای 5 نشانگر اهمیت است (B ، A و غیره). دراین میانگین ها فقط 1 (1=5-6)جفت تفاوت ندارند. پس از کمی سردرگمی مشخص شد ، درمان با homeopathicنقطه مقابل درمان با placebo است. این دقیقاً همان نتیجه ای است که قبلاً از مقایسه های دوتایی جدول توکی گرفتیم.
پس فعلاً همین است. امیدوارم این آموزش به شما کمک کند تا ANOVA را با آزمونهای تعقیبی با اطمینان اجرا کنید.
