فرضیه صفر ANOVA
آماره آزمون F
مفروضات ANOVA
اندازه اثر-Eta squared
آزمونهای آزمایشی ANOVA
ANOVA مخفف “analysis of variance” به معنای تحلیل واریانس یکی ازروش های آماری است برای آزمایش اینکه آیا میانگین(سه وبیشترکه می نویسیم: 3 (+)) جامعه همه برابر هستند دو سناریو ساده داریم:
1-انوا یک طرفه (one way ANOVA )برای مقایسه 3 (+) گروه بر روی 1 متغیر: آیا همه کودکان مدرسه A ، B و C دارای ضریب هوشی برابر هستند؟
2-اندازه گیری های مکرر ANOVA (Repeated measurement ANOVA) برای مقایسه 3 (+) متغیر در 1 گروه: آیا میانگین امتیاز نوشابه A ، B و C برای همه افراد برابر است؟
شکل زیر سوال اساسی را برای ANOVA یک طرفه نشان می دهد.

مثال ساده ONOVA یک طرفه
یک دانشمند می خواهد بداند آیا بچه های مدارس A ، B و C دارای میانگین ضریب هوشی یکسانی هستند. هر مدرسه 1000 فرزند دارد. برای آزمایش 3000 کودک زمان و هزینه زیادی لازم است. بنابراین یک نمونه تصادفی ساده با تعداد n = 10 کودک از هر مدرسه آزمایش می شود. بخشی از این داده ها – در زیرنشان داده شده است.(1)

جدول توصیفی
درست است ، بنابراین داده های ما شامل 3 نمونه از 10 کودک است که هر کدام نمره ضریب هوشی خود را دارند. اجرای یک جدول توصیف ساده بلافاصله میانگین نمره ضریب هوشی برای این نمونه ها را به ما می گوید. نتیجه در پاین نشان داده شده است.

برای شفاف سازی امور ، بیایید میانگین نمره ضریب هوشی هر مدرسه را در یک نمودار میله ای ساده بررسی کنیم.
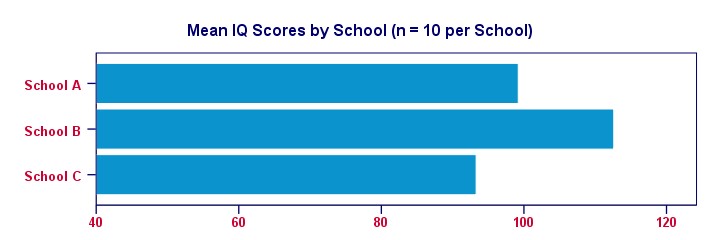
واضح است که نمونه ما از مدرسه B بالاترین ضریب هوشی را دارد – تقریبا 113 امتیاز. کمترین میانگین ضریب هوشی – حدود 93 امتیاز – برای مدرسه C دیده می شود.
اکنون ، این مسئله در اینجا وجود دارد: میانگین نمره ضریب هوشی ما فقط بر اساس نمونه های کوچکی از 10 کودک در هر مدرسه است. بنابراین آیا می توان گفت که 1000 کودک در هر مدرسه از ضریب هوشی یکسانی برخوردار هستند؟ شاید ما فقط به طور تصادفی از باهوش ترین کودکان مدرسه B و تنبل ترین کودکان از مدرسه C نمونه بگیریم؟ آیا واقع بینانه است؟ ما سعی خواهیم کرد و نشان خواهیم داد که این گفته – فرضیه صفر ما – با توجه به داده های ما معتبر نیست.
فرضیه صفر ANOVA
فرضیه صفر برای( هر) ANOVAبه آن معنی است که تمام جامعه برابر باشد.
اگر این این مسئله برقرار باشد، پس میانگین نمونه های ما احتمالاً تفاوت کمی خواهند داشت. از این گذشته، نمونه ها همیشه با جامعه ی خود کمی متفاوت هستند. با این حال، میانگین نمونه ها معمولا نباید خیلی تفاوت داشته باشد. بعید است تحت چنین نتیجه ای در فرضیه صفر میانگین جامعه برابر باشد. بنابراین اگر این را متوجه شویم، احتمالاً دیگر باور نخواهیم کرد که میانگین نمونه های جامعه ما برابر باشد.
مجموع مربعات ANOVA
بنابراین تفاوت میانگین3نمونه چقدر است؟ این اعداد تا چه اندازه از هم فاصله دارند؟ عددی که این رابه ما می گوید فقط واریانس است. بنابراین ما اساساً واریانس بین 3 میانگین نمونه خود را محاسبه خواهیم کرد. همانطور که از فرمولهای ANOVA متوجه میشوید، این کار با جمع مربع انحرافات بین 3 میانگین نمونه و میانگین کلی شروع می شود. نتیجه به عنوان مجموع مربعات بین یعنی “sum of squres between” یا” SSbetween” شناخته می شود.پس مجموع مربعات بین گروه ها هستند.
هر قدر مجموع مربعات بین گروه ها از مقدار کلی پراکندگی در میانگین نمونه ها بیشتر باشد نشان می دهد که میانگین نمونه ها تفاوت بیشتری دارد. و هرچه میانگین نمونه های ما متفاوت باشد، به احتمال زیاد جامعه ما نیز متفاوت است.

درجات آزادی و میانگین مربعات بین نمونه ها
هنگام محاسبه “عادی” واریانس، مقادیر مربع خود را بر درجه آزادی آن تقسیم می کنیم. هنگام مقایسه k میانگین، درجه آزادی(df)، برابراست با (k – 1). از تقسیم مجموع مربعات بین به (k – 1)، میانگین مربعات بین “MSbetween”بدست می آید. در واقع واریانس بین میانگین نمونه ها است. بنابراین میانگین مربعات بین نمونه ها نشان می دهد که میانگین نمونه ما تا چه اندازه متفاوت است(یا از هم فاصله دارند). هرچه واریانس بین میانگین ها بیشتر باشد، به احتمال زیاد میانگین جامعه ما نیز متفاوت است.
مجموع مربعات درون ANOVA
اگر میانگین جامعه ما واقعاً برابر باشد، پس چه تفاوتی بین، میانگین نمونه بین می توان به طورمنطقی انتظار داشت؟ خوب، این به واریانس موجود در زیرمجموعه ها بستگی دارد. شکل زیر این 3 سناریو را نشان می دهد.

3 هیستوگرام سمت چپ توزیع جامعه را برای ضریب هوشی در مدارس A ، B و C نشان می دهد که باریک بودن آنها نشان دهنده اختلاف کم در هر مدرسه است. اگر از هر مدرسه تعداد n = 10 دانش آموز بگیریم، آیا باید انتظار داشته باشیم که نمونه های بسیار متفاوتی داشته باشیم؟ احتمالاً نه. چرا؟ خوب، به دلیل اینکه واریانس کوچک در هر مدرسه، میانگین نمونه به میانگین جامعه نزدیک (برابر) خواهد بود. این هیستوگرام های باریک فضای زیادی برای معنی دار بودن و متفاوت بودن نمونه آنها باقی نمی گذارد. 3 هیستوگرام مناسب ترین حالت سناریوی مخالف را نشان می دهند: هیستوگرام ها گسترده هستند ، که نشان دهنده واریانس زیاد در هر مدرسه است. اگر ما از هر مدرسه تعداد n = 10 (یعنی حجم نمونه کم نسبت به جامعه)دانش آموز داشته باشیم .بطورخلاصه، اختلافات بیشتر در مدارس احتمالاً منجر بهa واریانس بیشتر بین میانگین نمونه در هر مدرسه.
ما اساساً واریانس جمعیت درون گروهی را از واریانس نمونه درون گروهی تخمین می زنیم. منطقی است ، درسته ؟ محاسبات دقیق در فرمول های ANOVA و این صفحه گوگل وجود دارد. به اختصار:
- مجموع مربعات درون SSwithin))مقدار کل پراکندگی درون گروه ها را نشان می دهد.
- درجه آزادی درون DFwithin)) برابرست با n – k))برای n مشاهدات و k گروه .
- میانگین مربعات درون (MSwithin )اساساً واریانس درون گروه هابرابرست با SSwithin / DFwithin
آماره آزمون ( F) ANOVA
بنابراین احتمال مساوی بودن جامعه چقدر است؟ این به 3 قسمت ازاطلاعات نمونه های ما بستگی دارد:
- واریانس بین میانگین نمونه MSbetween) )؛
- واریانس درون نمونه های ماMSwithin) )و
- اندازه های نمونه
ما اساساً همه این اطلاعات را به یک عدد واحد ترکیب می کنیم: آمار آزمون ما(F). نمودار زیر نشان می دهد که چگونه هر قسمت بر اماره ازمون تأثیر می گذارد.

خود آماره ازمون همیشه جالب نیست. با این حال ، می توانیم اهمیت آماری اماره ازمون را زمانی بدست آوریم که ازتوزیعFپیروی کند. این کار در صورت تحقق 3 فرض انجام می شود.
فرضیات ANOVA
فرضیه های ANOVA عبارتند از:
- مشاهدات مستقل؛
- نرمال بودن :متغیر نتیجه باید از توزیع نرمال در هر زیرمجموعه ای برخوردار باشد. طبیعی است که فقط برای اندازه های کوچک نمونه لازم است ، مثلاً n<20 در هر گروه.
- همگنی: واریانس های موجود در همه زیرمجموعه ها باید برابر باشند. همگنی تنها در مواردی مورد نیاز است که اندازه نمونه بسیار نابرابر باشد. در این حالت ، آزمایش لون نشان می دهد که آیا آن رابراورد کرده است.
اگر این فرضیات برقرار باشد ، اماره ازمون از یک توزیع F با درجه آزادی اماره بیرونی” DFbetween” و درجه ازادی اماره درونی” DFwithin” پیروی می کند نشان می دهدکه ایا ان رابراورد کرده است. در مثال ما -3 گروه باحجم n = 10 هر کدام دارای توزیع(2،27) F خواهد بود.
اهمیت آماری ANOVA
در مثال ما ،6.15 = (2،27) F . این مقدار F بزرگ دلیل بزرگی بر این است که فرضیه صفر ما –که همه مدارس دارای میانگین ضریب هوشی برابر هستند- درست نیست. اگر تمام فرضیات برآوردشوند ، F پیروی می کند از توزیع F نشان داده شده در زیر.

با توجه به این توزیع ، می توانیم اهمیت آماری را جستجو کنیم. ما معمولاً گزارش می دهیم: p = 0.006، 6.15 = (2،27) F اگر مدارس ما از ضریب هوشی یکسانی برخوردار باشند ، فقط 0.006 احتمال داردکه میانگین نمونه متفاوت یا بزرگتراز ان پیداکرد. ما معمولاً می گوییم چیزی “از نظر آماری معنی دار است”که0.05p < باشد.
نتیجه میگیریم: به نظر می رسد میانگین جامعه ما برابر نباشد. شکل زیر نشان می دهد که SPSS چگونه خروجی این مثال را ارائه می دهد.

اندازه اثر (جزئی) در مربع
نتیجه ای که تاکنون گرفته ایم این است که میانگین جامعه دقیقابرابر نیستند. اکنون ، “برابر نیست” چیز زیادی نمی گوید. مامی خواهم بدانیم دقیقا تفاوت میانگین ها چقدر است؟ عددی که فقط اندازه اثر را تخمین می زند. اندازه گیری اندازه اثر برای ANOVA جزئی درمربع است که به صورت η2 می نویسیم. * برای یک ANOVA یک طرفه ، مربع eta جزئی جزئی برابر با مربع eta ساده است.
از نظر فنی ، (جزئی)درمربع عبارتست از
نسبت واریانس توسط یک عامل به حساب می آید. برخی از قوانین کلی این است که
- 0.01η2> نشان دهنده یک اثر کوچک است.
- · 0.06 η2>یک اثر متوسط را نشان می دهد.
- · 0.14 η2> نشان دهنده یک تأثیر بزرگ است.
- محاسبه دقیق مربع eta در بخش فرمول ها نشان داده شده است. در حال حاضر ، کافی است که بگوییم برای مثال ما η2 = 0.31. این بزرگی اندازه اثربزرگ را توضیح می دهد که چرا آزمون F ما با وجود اندازه نمونه های بسیار کوچک n = 10 در هر مدرسه ، از نظر آماری قابل توجه است.
تست های HSD Post Hoc توکی
تا کنون ، ما از آزمون F نتیجه گرفتیم که به نظر می رسد میانگین جامعه ما (همه) برابر باشد. اندازه اثر ، η2 ، به ما گفت که تفاوت زیاد است. اگرچه یک سوال بدون پاسخ که دقیقاً کدام یک از آنها متفاوت است وجوددارد؟ باوجود الگوهای مختلف از میانگین نمونه ممکن است همه نتایج بامقدارFدقیقامساوی باشند . شکل زیر با چند سناریو احتمالی این نکته را نشان می دهد.

یک روش می تواند اجرای آزمونهای t نمونه های مستقل بر روی همه جفت های نمونه باشد. برای 3 میانگین ، A-B ، A-C و B-C خواهد بود. با این حال ، هرچه تعداد میانگین های مقایسه شده ما زیادمی شود، تعداد همه جفت های ممکن نیزبه سرعت افزایش می یابد. * هر آزمون t احتمال دارد که نتیجه گیری نادرستی را انجام دهد. بنابراین هرچه تست های t بیشتری انجام دهیم ، خطر نتیجه گیری حداقل یک نتیجه اشتباه بیشتراست
رایج ترین راه حل برای این مشکل استفاده از روش HSD Tukey (مخفف “تفاوت صادقانه قابل توجه”) است. می توانید تصور کنید که این همه تست های t ممکن است که نتایج آن با نوعی اصلاح بونفرونی اصلاح شده اما محافظه کارانه کمترباشد. شکل زیر خروجی حاصل از HSD توکی در SPSS را نشان می دهد.

توکی HSD به عنوان یک آزمون تعقیبی شناخته می شود. “Post hoc” لاتین است و در لغت به معنای “پس از آن” است. این بدان دلیل است که آنها پس ازاینکه میانگین ازمون F نشان می دهد که همه میانگین ها برابر نیستند اجرا می شوند. من کاملاً با این کنوانسیون موافق نیستم زیرا
آزمونهای تعقیبی ممکن است تفاوتها را نشان ندهد در حالی که آزمون F اصلی نشان می دهد؛
آزمونهای تعقیبی ممکن است تفاوتها را نشان دهند در حالیکه آزمون F اصلی اینگونه نیست. بگویید من 5میانگین رامقایسه می کنم: A ، B ، C و D برابر هستند اما E بسیار بزرگتر از سایرین است. در این حالت ، تفاوت بزرگ بین E و سایر میانگین ها هنگام آزمایش در صورت برابر بودن همه میانگین ها به شدت کاهش می یابد. بنابراین در این مورد به طورکلی آزمون F ممكن است که هیچ تفاوتی را نشان نمی دهد. در حالی که آزمونهای تعقیبی نشان می دهند.
آخرین موضوع ، آزمونهای تعقیبی دیگری نیز وجود دارد. برخی به فرض همگنی احتیاج دارند و برخی دیگر این کار را نمی کنند. شکل زیر چند نمونه را نشان می دهد.

فرمول های اساسی – ANOVA
برای کامل بودن ، فرمول های اصلی استفاده شده برای ANOVA یک طرفه را در مثال خود لیست می کنیم. می توانید آنها را در این صفحه مشاهده کنید. ما با واریانس بین گروه ها شروع خواهیم کرد:
جایی که
- X—j X—میانگین گروه را نشان می دهد.
- · X¯¯¯¯X¯ میانگین کلی است.
- · njnj اندازه نمونه در هر گروه است.
برای مثال ما ، این نتیجه در
S
S
b
e
t
w
e
e
n
=
10
(
99.2
−
101.7
)
2
+
10
(
112.6
−
101.7
)
2
+
10
(
93.3
−
101.7
)
2
=
1956.2
SSbetween = 10 (99.2−101.7) 2 + 10 (112.6−101.7) 2 + 10 (93.3−101.7) )2 = 1956.2
بعد ، برای mmگروه ،
df_{between} = m – 1
بنابراین
برای داده های مثال ما dfbetweendfbetween = 3 – 1 = 2
MSbetween = SSbetweendfbetweenMSbetween = SSbetweendfbetween برای مثال ما ، این خواهد بود
1956.22 = 978.11956.22 = 978.1
اکنون واریانس درون گروه ها رابررسی می کنیم. اول از همه،
SSwithin = Σ (Xi − X¯¯¯¯j) 2 SSwithin = Σ (Xi − X¯j) 2
جایی که
X—j X—میانگین گروه را نشان می دهد؛
XiXi یک مشاهده فردی را نشان می دهد (“نقطه داده”).
برای مثال ما ، داریم
\\(\\)
برای nn مشاهدات مستقل و mmگروه های ،
dfwithin = n − mdfwithin = n-m
بنابراین برای مثال ما30-3=27 است
MSwithin = SSwithindfwithinMSwithin = SSwithindfwithin
برای مثال ما ، 159= 1594294.127 = 4294.127
اکنون آماده محاسبه آمار F هستیم:
F = MSbetweenMSwithin F = MSbetweenMSwithin
که منجر به 6.15 = 6.15978.1159 = 978.1159
سرانجام، P = P (F (2،27)> 6.15) = 0.0063P = P (F (2،27)> 6.15) = 0.0063
در صورت تمایل ، اندازه اثر η2 به این صورت محاسبه می شود
Effectsizeη2 = SSbetweenSSbetween + SSwithinEffectsizeη2 = SSbetweenSSbetween + SSwithin
1956.21956.2+4294.1=0.311956.21956.2+429.4=0.31برای مثال ماعبارت است
با تشکر از شما برای خواندن
فرضیه صفر ANOVA
آماره آزمون F
مفروضات ANOVA
اندازه اثر-Eta squared
$$SS_{within} = (90 – 99.2)^2 + (87 – 99.2)^2 + … + (96 – 93.3)^2 = 4294.1$$
آزمونهای آزمایشی ANOVA

مثال ساده ONOVA یک طرفه
یک دانشمند می خواهد بداند آیا بچه های مدارس A ، B و C دارای میانگین ضریب هوشی یکسانی هستند. هر مدرسه 1000 فرزند دارد. برای آزمایش 3000 کودک زمان و هزینه زیادی لازم است. بنابراین یک نمونه تصادفی ساده با تعداد n = 10 کودک از هر مدرسه آزمایش می شود. بخشی از این داده ها – در زیرنشان داده شده است.(1)

جدول توصیفی
درست است ، بنابراین داده های ما شامل 3 نمونه از 10 کودک است که هر کدام نمره ضریب هوشی خود را دارند. اجرای یک جدول توصیف ساده بلافاصله میانگین نمره ضریب هوشی برای این نمونه ها را به ما می گوید. نتیجه در پاین نشان داده شده است.

برای شفاف سازی امور ، بیایید میانگین نمره ضریب هوشی هر مدرسه را در یک نمودار میله ای ساده تجسم کنیم.

واضح است که نمونه ما از مدرسه B بالاترین ضریب هوشی را دارد – تقریبا 113 امتیاز. کمترین میانگین ضریب هوشی – حدود 93 امتیاز – برای مدرسه C دیده می شود.
اکنون ، این مسئله در اینجا وجود دارد: میانگین نمره ضریب هوشی ما فقط بر اساس نمونه های کوچکی از 10 کودک در هر مدرسه است. بنابراین آیا می توان گفت که 1000 کودک در هر مدرسه از ضریب هوشی یکسانی برخوردار هستند؟ شاید ما فقط به طور تصادفی از باهوش ترین کودکان مدرسه B و احمق ترین کودکان از مدرسه C نمونه بگیریم؟ آیا واقع بینانه است؟ ما سعی خواهیم کرد و نشان خواهیم داد که این گفته – فرضیه صفر ما – با توجه به داده های ما معتبر نیست.
فرضیه صفر ANOVA –
فرضیه صفر برای( هر) ANOVAبه آن معنی است که تمام جامعه برابر باشد.
اگر این این مسیله برقرار باشد ، پس میانگین نمونه ما احتمالاً کمی متفاوت خواهد بود. از این گذشته ، نمونه ها همیشه با جامعه ای که نشان می دهند کمی متفاوت است. با این حال ، میانگین نمونه معمولا نباید خیلی تفاوت داشته باشد. بعید است تحت چنین نتیجه ای در فرضیه صفر میانگین جامعه برابرباشد. بنابراین اگر این را پیدا کنیم ، احتمالاً دیگر باور نخواهیم کرد که میانگین جامعه ما برابر است.
مجموع مربعات ANOVA –
بنابراین تفاوت میانگین3نمونه چقدر است؟ این اعداد تا چه اندازه از هم فاصله دارند؟ عددی که این رابه ما می گوید فقط واریانس است. بنابراین ما اساساً واریانس بین 3 میانگین نمونه خود را محاسبه خواهیم کرد.
همانطور که از فرمولهای ANOVA متوجه میشوید، این کار با جمع انحرافات مربع بین 3 میانگین نمونه و میانگین کلی شروع می شود. نتیجه به عنوان مجموع مربعات بین یعنی “sum of squres between” یا” SSbetween” شناخته می شود.پس مجموع مربعات بین گروه ها هستند.
مقدار کلی پراکندگی در میانگین نمونه. هر عدد بزرگ تر یامساوی مجموع مربعات بین نشان می دهد که میانگین نمونه تفاوت بیشتری دارد. و هرچه میانگین نمونه های ما متفاوت باشد ، به احتمال زیاد جامعه ما نیز متفاوت است.

درجات آزادی و میانگین مربعات بین
هنگام محاسبه “عادی” واریانس ، مقادیر مربع خود را بر درجه آزادی آن تقسیم می کنیم .هنگام مقایسه k میانگین ،درجه آزادی(df) ،برابراست با(k – 1).
ازتقسیم مجموع مربعات بین به (k – 1) ،میانگین مربعات بین “MSbetween”بدست می اید.
در واقع واریانس بین میانگین نمونه است. بنابراین میانگین مربعات بین نشان می دهد که میانگین نمونه ما تا چه اندازه متفاوت است (یا از هم فاصله دارند). هرچه واریانس بین میانگین هابیشتر باشد ، به احتمال زیاد میانگین جمعیت ما نیز متفاوت است.
مجموع مربعات درون ANOVA –
اگر میانگین جامعه ما واقعاً برابر باشد ، پس چه تفاوتی بین، میانگین نمونه بین می توان به طورمنطقی انتظار داشت؟ خوب ، این به واریانس موجود در زیرمجموعه ها بستگی دارد. شکل زیر این 3 سناریو را نشان می دهد.

3 هیستوگرام سمت چپ توزیع جامعه را برای ضریب هوشی در مدارس A ، B و C نشان می دهد که باریک بودن آنها نشان دهنده اختلاف کم در هر مدرسه است. اگر از هر مدرسه تعداد n = 10 دانش آموز بگیریم ، آیا باید انتظار داشته باشیم که نمونه های بسیار متفاوتی داشته باشیم؟ احتمالاً نه. چرا؟ خوب ، به دلیل اینکه واریانس کوچک در هر مدرسه ، میانگین نمونه به میانگین جامعه نزدیک (برابر) خواهد بود. این هیستوگرام های باریک فضای زیادی برای معنی دار بودن و متفاوت بودن نمونه آنها باقی نمی گذارد.
3 هیستوگرام مناسب ترین حالت سناریوی مخالف را نشان می دهند: هیستوگرام ها گسترده هستند ، که نشان دهنده واریانس زیاد در هر مدرسه است. اگر ما از هر مدرسه تعداد n = 10 (یعنی حجم نمونه کم نسبت به جامعه)دانش آموز داشته باشیم .بطورخلاصه،
اختلافات بیشتر در مدارس احتمالاً منجر بهa واریانس بیشتر بین میانگین نمونه در هر مدرسه.
ما اساساً واریانس جمعیت درون گروهی را از واریانس نمونه درون گروهی تخمین می زنیم. منطقی است ، درسته ؟ محاسبات دقیق در فرمول های ANOVA و این صفحه گوگل وجود دارد. به اختصار:
- مجموع مربعات درون SSwithin))مقدار کل پراکندگی درون گروه ها را نشان می دهد.
- درجه آزادی درون DFwithin)) برابرست با n – k))برای n مشاهدات و k گروه .
- میانگین مربعات درون (MSwithin )اساساً واریانس درون گروه هابرابرست با SSwithin / DFwithin
آماره آزمون ( F) ANOVA
بنابراین احتمال مساوی بودن جامعه چقدر است؟ این به 3 قسمت ازاطلاعات نمونه های ما بستگی دارد:
- واریانس بین میانگین نمونه MSbetween) )؛
- واریانس درون نمونه های ماMSwithin) )و
- اندازه های نمونه
ما اساساً همه این اطلاعات را به یک عدد واحد ترکیب می کنیم: آمار آزمون ما(F).
نمودار زیر نشان می دهد که چگونه هر قسمت بر اماره ازمون تأثیر می گذارد.

خوداماره ازمون همیشه جالب نیست. با این حال ، می توانیم اهمیت آماری اماره ازمون را زمانی بدست آوریم که ازتوزیعFپیروی کند. این کار در صورت تحقق 3 فرض انجام می شود.
فرضیات ANOVA-
فرضیه های ANOVA عبارتند از:
- مشاهدات مستقل؛
- · نرمال بودن :متغیر نتیجه باید از توزیع نرمال در هر زیرمجموعه ای برخوردار باشد. طبیعی است که فقط برای اندازه های کوچک نمونه لازم است ، مثلاً n<20 در هر گروه.
- همگنی: واریانس های موجود در همه زیرمجموعه ها باید برابر باشند. همگنی تنها در مواردی مورد نیاز است که اندازه نمونه بسیار نابرابر باشد. در این حالت ، آزمایش لون نشان می دهد که آیا آن رابراورد کرده است.
اگر این فرضیات برقرار باشد ، اماره ازمون از یک توزیع F با درجه آزادی اماره بیرونی” DFbetween” و درجه ازادی اماره درونی” DFwithin” پیروی می کند نشان می دهدکه ایا ان رابراورد کرده است. در مثال ما -3 گروه باحجم n = 10 هر کدام دارای توزیع(2،27) F خواهد بود.
اهمیت آماری ANOVA –
در مثال ما ،6.15 = (2،27) F . این مقدار F بزرگ دلیل بزرگی بر این است که فرضیه صفر ما –که همه مدارس دارای میانگین ضریب هوشی برابر هستند- درست نیست. اگر تمام فرضیات برآوردشوند ، F پیروی می کند از توزیع F نشان داده شده در زیر.

با توجه به این توزیع ، می توانیم اهمیت آماری را جستجو کنیم. ما معمولاً گزارش می دهیم: p = 0.006، 6.15 = (2،27) F اگر مدارس ما از ضریب هوشی یکسانی برخوردار باشند ، فقط 0.006 احتمال داردکه میانگین نمونه متفاوت یا بزرگتراز ان پیداکرد. ما معمولاً می گوییم چیزی “از نظر آماری معنی دار است”که0.05p < باشد.
نتیجه میگیریم: به نظر می رسد میانگین جامعه ما برابر نباشد. شکل زیر نشان می دهد که SPSS چگونه خروجی این مثال را ارائه می دهد.

اندازه اثر (جزئی) در مربع
نتیجه ای که تاکنون گرفته ایم این است که میانگین جامعه دقیقابرابر نیستند. اکنون ، “برابر نیست” چیز زیادی نمی گوید. مامی خواهم بدانیم دقیقا تفاوت میانگین ها چقدر است؟ عددی که فقط اندازه اثر را تخمین می زند. اندازه گیری اندازه اثر برای ANOVA جزئی درمربع است که به صورت η2 می نویسیم. * برای یک ANOVA یک طرفه ، مربع eta جزئی جزئی برابر با مربع eta ساده است.
از نظر فنی ، (جزئی)درمربع عبارتست از
نسبت واریانس توسط یک عامل به حساب می آید. برخی از قوانین کلی این است که
- 0.01η2> نشان دهنده یک اثر کوچک است.
- · 0.06 η2>یک اثر متوسط را نشان می دهد.
- · 0.14 η2> نشان دهنده یک تأثیر بزرگ است.
- محاسبه دقیق مربع eta در بخش فرمول ها نشان داده شده است. در حال حاضر ، کافی است که بگوییم برای مثال ما η2 = 0.31. این بزرگی اندازه اثربزرگ را توضیح می دهد که چرا آزمون F ما با وجود اندازه نمونه های بسیار کوچک n = 10 در هر مدرسه ، از نظر آماری قابل توجه است.
تست های HSD Post Hoc توکی
تا کنون ، ما از آزمون F نتیجه گرفتیم که به نظر می رسد میانگین جامعه ما (همه) برابر باشد. اندازه اثر ، η2 ، به ما گفت که تفاوت زیاد است. اگرچه یک سوال بدون پاسخ که دقیقاً کدام یک از آنها متفاوت است وجوددارد؟ باوجود الگوهای مختلف از میانگین نمونه ممکن است همه نتایج بامقدارFدقیقامساوی باشند . شکل زیر با چند سناریو احتمالی این نکته را نشان می دهد.

یک روش می تواند اجرای آزمونهای t نمونه های مستقل بر روی همه جفت های نمونه باشد. برای 3 میانگین ، A-B ، A-C و B-C خواهد بود. با این حال ، هرچه تعداد میانگین های مقایسه شده ما زیادمی شود، تعداد همه جفت های ممکن نیزبه سرعت افزایش می یابد. * هر آزمون t احتمال دارد که نتیجه گیری نادرستی را انجام دهد. بنابراین هرچه تست های t بیشتری انجام دهیم ، خطر نتیجه گیری حداقل یک نتیجه اشتباه بیشتراست
رایج ترین راه حل برای این مشکل استفاده از روش HSD Tukey (مخفف “تفاوت صادقانه قابل توجه”) است. می توانید تصور کنید که این همه تست های t ممکن است که نتایج آن با نوعی اصلاح بونفرونی اصلاح شده اما محافظه کارانه کمترباشد. شکل زیر خروجی حاصل از HSD توکی در SPSS را نشان می دهد.

توکی HSD به عنوان یک آزمون تعقیبی شناخته می شود. “Post hoc” لاتین است و در لغت به معنای “پس از آن” است. این بدان دلیل است که آنها پس ازاینکه میانگین ازمون F نشان می دهد که همه میانگین ها برابر نیستند اجرا می شوند. من کاملاً با این کنوانسیون موافق نیستم زیرا
آزمونهای تعقیبی ممکن است تفاوتها را نشان ندهد در حالی که آزمون F اصلی نشان می دهد؛
آزمونهای تعقیبی ممکن است تفاوتها را نشان دهند در حالیکه آزمون F اصلی اینگونه نیست. بگویید من 5میانگین رامقایسه می کنم: A ، B ، C و D برابر هستند اما E بسیار بزرگتر از سایرین است. در این حالت ، تفاوت بزرگ بین E و سایر میانگین ها هنگام آزمایش در صورت برابر بودن همه میانگین ها به شدت کاهش می یابد. بنابراین در این مورد به طورکلی آزمون F ممكن است که هیچ تفاوتی را نشان نمی دهد. در حالی که آزمونهای تعقیبی نشان می دهند.
آخرین موضوع ، آزمونهای تعقیبی دیگری نیز وجود دارد. برخی به فرض همگنی احتیاج دارند و برخی دیگر این کار را نمی کنند. شکل زیر چند نمونه را نشان می دهد.

فرمول های اساسی – ANOVA
برای کامل بودن ، فرمول های اصلی استفاده شده برای ANOVA یک طرفه را در مثال خود لیست می کنیم. می توانید آنها را در این صفحه مشاهده کنید. ما با واریانس بین گروه ها شروع خواهیم کرد:
جایی که
- X—j X—میانگین گروه را نشان می دهد.
- · X¯¯¯¯X¯ میانگین کلی است.
- · njnj اندازه نمونه در هر گروه است.
برای مثال ما ، این نتیجه در
S
S
b
e
t
w
e
e
n
=
10
(
99.2
−
101.7
)
2
+
10
(
112.6
−
101.7
)
2
+
10
(
93.3
−
101.7
)
2
=
1956.2
SSbetween = 10 (99.2−101.7) 2 + 10 (112.6−101.7) 2 + 10 (93.3−101.7) )2 = 1956.2
بعد ، برای mmگروه ،
df_{between} = m – 1
بنابراین
برای داده های مثال ما dfbetweendfbetween = 3 – 1 = 2
MSbetween = SSbetweendfbetweenMSbetween = SSbetweendfbetween برای مثال ما ، این خواهد بود
1956.22 = 978.11956.22 = 978.1
اکنون واریانس درون گروه ها رابررسی می کنیم. اول از همه،
SSwithin = Σ (Xi − X¯¯¯¯j) 2 SSwithin = Σ (Xi − X¯j) 2
جایی که
X—j X—میانگین گروه را نشان می دهد؛
XiXi یک مشاهده فردی را نشان می دهد (“نقطه داده”).
برای مثال ما ، داریم
برای nn مشاهدات مستقل و mmگروه های ،
dfwithin = n − mdfwithin = n-m
بنابراین برای مثال ما30-3=27 است
MSwithin = SSwithindfwithinMSwithin = SSwithindfwithin
برای مثال ما ، 159= 1594294.127 = 4294.127
اکنون آماده محاسبه آمار F هستیم:
F = MSbetweenMSwithin F = MSbetweenMSwithin
که منجر به 6.15 = 6.15978.1159 = 978.1159
سرانجام، P = P (F (2،27)> 6.15) = 0.0063P = P (F (2،27)> 6.15) = 0.0063
در صورت تمایل ، اندازه اثر η2 به این صورت محاسبه می شود
Effectsizeη2 = SSbetweenSSbetween + SSwithinEffectsizeη2 = SSbetweenSSbetween + SSwithin
1956.21956.2+4294.1=0.311956.21956.2+429.4=0.31برای مثال ماعبارت است
با تشکر از شما برای خواندن
فرضیه صفر ANOVA
آماره آزمون F
مفروضات ANOVA
اندازه اثر-Eta squared
آزمونهای آزمایشی ANOVA

مثال ساده ONOVA یک طرفه
یک دانشمند می خواهد بداند آیا بچه های مدارس A ، B و C دارای میانگین ضریب هوشی یکسانی هستند. هر مدرسه 1000 فرزند دارد. برای آزمایش 3000 کودک زمان و هزینه زیادی لازم است. بنابراین یک نمونه تصادفی ساده با تعداد n = 10 کودک از هر مدرسه آزمایش می شود. بخشی از این داده ها – در زیرنشان داده شده است.(1)

جدول توصیفی
درست است ، بنابراین داده های ما شامل 3 نمونه از 10 کودک است که هر کدام نمره ضریب هوشی خود را دارند. اجرای یک جدول توصیف ساده بلافاصله میانگین نمره ضریب هوشی برای این نمونه ها را به ما می گوید. نتیجه در پاین نشان داده شده است.

برای شفاف سازی امور ، بیایید میانگین نمره ضریب هوشی هر مدرسه را در یک نمودار میله ای ساده تجسم کنیم.

واضح است که نمونه ما از مدرسه B بالاترین ضریب هوشی را دارد – تقریبا 113 امتیاز. کمترین میانگین ضریب هوشی – حدود 93 امتیاز – برای مدرسه C دیده می شود.
اکنون ، این مسئله در اینجا وجود دارد: میانگین نمره ضریب هوشی ما فقط بر اساس نمونه های کوچکی از 10 کودک در هر مدرسه است. بنابراین آیا می توان گفت که 1000 کودک در هر مدرسه از ضریب هوشی یکسانی برخوردار هستند؟ شاید ما فقط به طور تصادفی از باهوش ترین کودکان مدرسه B و احمق ترین کودکان از مدرسه C نمونه بگیریم؟ آیا واقع بینانه است؟ ما سعی خواهیم کرد و نشان خواهیم داد که این گفته – فرضیه صفر ما – با توجه به داده های ما معتبر نیست.
فرضیه صفر ANOVA –
فرضیه صفر برای( هر) ANOVAبه آن معنی است که تمام جامعه برابر باشد.
اگر این این مسیله برقرار باشد ، پس میانگین نمونه ما احتمالاً کمی متفاوت خواهد بود. از این گذشته ، نمونه ها همیشه با جامعه ای که نشان می دهند کمی متفاوت است. با این حال ، میانگین نمونه معمولا نباید خیلی تفاوت داشته باشد. بعید است تحت چنین نتیجه ای در فرضیه صفر میانگین جامعه برابرباشد. بنابراین اگر این را پیدا کنیم ، احتمالاً دیگر باور نخواهیم کرد که میانگین جامعه ما برابر است.
مجموع مربعات ANOVA –
بنابراین تفاوت میانگین3نمونه چقدر است؟ این اعداد تا چه اندازه از هم فاصله دارند؟ عددی که این رابه ما می گوید فقط واریانس است. بنابراین ما اساساً واریانس بین 3 میانگین نمونه خود را محاسبه خواهیم کرد.
همانطور که از فرمولهای ANOVA متوجه میشوید، این کار با جمع انحرافات مربع بین 3 میانگین نمونه و میانگین کلی شروع می شود. نتیجه به عنوان مجموع مربعات بین یعنی “sum of squres between” یا” SSbetween” شناخته می شود.پس مجموع مربعات بین گروه ها هستند.
مقدار کلی پراکندگی در میانگین نمونه. هر عدد بزرگ تر یامساوی مجموع مربعات بین نشان می دهد که میانگین نمونه تفاوت بیشتری دارد. و هرچه میانگین نمونه های ما متفاوت باشد ، به احتمال زیاد جامعه ما نیز متفاوت است.

درجات آزادی و میانگین مربعات بین
هنگام محاسبه “عادی” واریانس ، مقادیر مربع خود را بر درجه آزادی آن تقسیم می کنیم .هنگام مقایسه k میانگین ،درجه آزادی(df) ،برابراست با(k – 1).
ازتقسیم مجموع مربعات بین به (k – 1) ،میانگین مربعات بین “MSbetween”بدست می اید.
در واقع واریانس بین میانگین نمونه است. بنابراین میانگین مربعات بین نشان می دهد که میانگین نمونه ما تا چه اندازه متفاوت است (یا از هم فاصله دارند). هرچه واریانس بین میانگین هابیشتر باشد ، به احتمال زیاد میانگین جمعیت ما نیز متفاوت است.
مجموع مربعات درون ANOVA –
اگر میانگین جامعه ما واقعاً برابر باشد ، پس چه تفاوتی بین، میانگین نمونه بین می توان به طورمنطقی انتظار داشت؟ خوب ، این به واریانس موجود در زیرمجموعه ها بستگی دارد. شکل زیر این 3 سناریو را نشان می دهد.

3 هیستوگرام سمت چپ توزیع جامعه را برای ضریب هوشی در مدارس A ، B و C نشان می دهد که باریک بودن آنها نشان دهنده اختلاف کم در هر مدرسه است. اگر از هر مدرسه تعداد n = 10 دانش آموز بگیریم ، آیا باید انتظار داشته باشیم که نمونه های بسیار متفاوتی داشته باشیم؟ احتمالاً نه. چرا؟ خوب ، به دلیل اینکه واریانس کوچک در هر مدرسه ، میانگین نمونه به میانگین جامعه نزدیک (برابر) خواهد بود. این هیستوگرام های باریک فضای زیادی برای معنی دار بودن و متفاوت بودن نمونه آنها باقی نمی گذارد.
3 هیستوگرام مناسب ترین حالت سناریوی مخالف را نشان می دهند: هیستوگرام ها گسترده هستند ، که نشان دهنده واریانس زیاد در هر مدرسه است. اگر ما از هر مدرسه تعداد n = 10 (یعنی حجم نمونه کم نسبت به جامعه)دانش آموز داشته باشیم .بطورخلاصه،
اختلافات بیشتر در مدارس احتمالاً منجر بهa واریانس بیشتر بین میانگین نمونه در هر مدرسه.
ما اساساً واریانس جمعیت درون گروهی را از واریانس نمونه درون گروهی تخمین می زنیم. منطقی است ، درسته ؟ محاسبات دقیق در فرمول های ANOVA و این صفحه گوگل وجود دارد. به اختصار:
- مجموع مربعات درون SSwithin))مقدار کل پراکندگی درون گروه ها را نشان می دهد.
- درجه آزادی درون DFwithin)) برابرست با n – k))برای n مشاهدات و k گروه .
- میانگین مربعات درون (MSwithin )اساساً واریانس درون گروه هابرابرست با SSwithin / DFwithin
آماره آزمون ( F) ANOVA
بنابراین احتمال مساوی بودن جامعه چقدر است؟ این به 3 قسمت ازاطلاعات نمونه های ما بستگی دارد:
- واریانس بین میانگین نمونه MSbetween) )؛
- واریانس درون نمونه های ماMSwithin) )و
- اندازه های نمونه
ما اساساً همه این اطلاعات را به یک عدد واحد ترکیب می کنیم: آمار آزمون ما(F).
نمودار زیر نشان می دهد که چگونه هر قسمت بر اماره ازمون تأثیر می گذارد.

خوداماره ازمون همیشه جالب نیست. با این حال ، می توانیم اهمیت آماری اماره ازمون را زمانی بدست آوریم که ازتوزیعFپیروی کند. این کار در صورت تحقق 3 فرض انجام می شود.
فرضیات ANOVA-
فرضیه های ANOVA عبارتند از:
- مشاهدات مستقل؛
- · نرمال بودن :متغیر نتیجه باید از توزیع نرمال در هر زیرمجموعه ای برخوردار باشد. طبیعی است که فقط برای اندازه های کوچک نمونه لازم است ، مثلاً n<20 در هر گروه.
- همگنی: واریانس های موجود در همه زیرمجموعه ها باید برابر باشند. همگنی تنها در مواردی مورد نیاز است که اندازه نمونه بسیار نابرابر باشد. در این حالت ، آزمایش لون نشان می دهد که آیا آن رابراورد کرده است.
اگر این فرضیات برقرار باشد ، اماره ازمون از یک توزیع F با درجه آزادی اماره بیرونی” DFbetween” و درجه ازادی اماره درونی” DFwithin” پیروی می کند نشان می دهدکه ایا ان رابراورد کرده است. در مثال ما -3 گروه باحجم n = 10 هر کدام دارای توزیع(2،27) F خواهد بود.
اهمیت آماری ANOVA –
در مثال ما ،6.15 = (2،27) F . این مقدار F بزرگ دلیل بزرگی بر این است که فرضیه صفر ما –که همه مدارس دارای میانگین ضریب هوشی برابر هستند- درست نیست. اگر تمام فرضیات برآوردشوند ، F پیروی می کند از توزیع F نشان داده شده در زیر.

با توجه به این توزیع ، می توانیم اهمیت آماری را جستجو کنیم. ما معمولاً گزارش می دهیم: p = 0.006، 6.15 = (2،27) F اگر مدارس ما از ضریب هوشی یکسانی برخوردار باشند ، فقط 0.006 احتمال داردکه میانگین نمونه متفاوت یا بزرگتراز ان پیداکرد. ما معمولاً می گوییم چیزی “از نظر آماری معنی دار است”که0.05p < باشد.
نتیجه میگیریم: به نظر می رسد میانگین جامعه ما برابر نباشد. شکل زیر نشان می دهد که SPSS چگونه خروجی این مثال را ارائه می دهد.

اندازه اثر (جزئی) در مربع
نتیجه ای که تاکنون گرفته ایم این است که میانگین جامعه دقیقابرابر نیستند. اکنون ، “برابر نیست” چیز زیادی نمی گوید. مامی خواهم بدانیم دقیقا تفاوت میانگین ها چقدر است؟ عددی که فقط اندازه اثر را تخمین می زند. اندازه گیری اندازه اثر برای ANOVA جزئی درمربع است که به صورت η2 می نویسیم. * برای یک ANOVA یک طرفه ، مربع eta جزئی جزئی برابر با مربع eta ساده است.
از نظر فنی ، (جزئی)درمربع عبارتست از
نسبت واریانس توسط یک عامل به حساب می آید. برخی از قوانین کلی این است که
- 0.01η2> نشان دهنده یک اثر کوچک است.
- · 0.06 η2>یک اثر متوسط را نشان می دهد.
- · 0.14 η2> نشان دهنده یک تأثیر بزرگ است.
- محاسبه دقیق مربع eta در بخش فرمول ها نشان داده شده است. در حال حاضر ، کافی است که بگوییم برای مثال ما η2 = 0.31. این بزرگی اندازه اثربزرگ را توضیح می دهد که چرا آزمون F ما با وجود اندازه نمونه های بسیار کوچک n = 10 در هر مدرسه ، از نظر آماری قابل توجه است.
تست های HSD Post Hoc توکی
تا کنون ، ما از آزمون F نتیجه گرفتیم که به نظر می رسد میانگین جامعه ما (همه) برابر باشد. اندازه اثر ، η2 ، به ما گفت که تفاوت زیاد است. اگرچه یک سوال بدون پاسخ که دقیقاً کدام یک از آنها متفاوت است وجوددارد؟ باوجود الگوهای مختلف از میانگین نمونه ممکن است همه نتایج بامقدارFدقیقامساوی باشند . شکل زیر با چند سناریو احتمالی این نکته را نشان می دهد.

یک روش می تواند اجرای آزمونهای t نمونه های مستقل بر روی همه جفت های نمونه باشد. برای 3 میانگین ، A-B ، A-C و B-C خواهد بود. با این حال ، هرچه تعداد میانگین های مقایسه شده ما زیادمی شود، تعداد همه جفت های ممکن نیزبه سرعت افزایش می یابد. * هر آزمون t احتمال دارد که نتیجه گیری نادرستی را انجام دهد. بنابراین هرچه تست های t بیشتری انجام دهیم ، خطر نتیجه گیری حداقل یک نتیجه اشتباه بیشتراست
رایج ترین راه حل برای این مشکل استفاده از روش HSD Tukey (مخفف “تفاوت صادقانه قابل توجه”) است. می توانید تصور کنید که این همه تست های t ممکن است که نتایج آن با نوعی اصلاح بونفرونی اصلاح شده اما محافظه کارانه کمترباشد. شکل زیر خروجی حاصل از HSD توکی در SPSS را نشان می دهد.

توکی HSD به عنوان یک آزمون تعقیبی شناخته می شود. “Post hoc” لاتین است و در لغت به معنای “پس از آن” است. این بدان دلیل است که آنها پس ازاینکه میانگین ازمون F نشان می دهد که همه میانگین ها برابر نیستند اجرا می شوند. من کاملاً با این کنوانسیون موافق نیستم زیرا
آزمونهای تعقیبی ممکن است تفاوتها را نشان ندهد در حالی که آزمون F اصلی نشان می دهد؛
آزمونهای تعقیبی ممکن است تفاوتها را نشان دهند در حالیکه آزمون F اصلی اینگونه نیست. بگویید من 5میانگین رامقایسه می کنم: A ، B ، C و D برابر هستند اما E بسیار بزرگتر از سایرین است. در این حالت ، تفاوت بزرگ بین E و سایر میانگین ها هنگام آزمایش در صورت برابر بودن همه میانگین ها به شدت کاهش می یابد. بنابراین در این مورد به طورکلی آزمون F ممكن است که هیچ تفاوتی را نشان نمی دهد. در حالی که آزمونهای تعقیبی نشان می دهند.
آخرین موضوع ، آزمونهای تعقیبی دیگری نیز وجود دارد. برخی به فرض همگنی احتیاج دارند و برخی دیگر این کار را نمی کنند. شکل زیر چند نمونه را نشان می دهد.

فرمول های اساسی – ANOVA
برای کامل بودن ، فرمول های اصلی استفاده شده برای ANOVA یک طرفه را در مثال خود لیست می کنیم. می توانید آنها را در این صفحه مشاهده کنید. ما با واریانس بین گروه ها شروع خواهیم کرد:
جایی که
- X—j X—میانگین گروه را نشان می دهد.
- · X¯¯¯¯X¯ میانگین کلی است.
- · njnj اندازه نمونه در هر گروه است.
برای مثال ما ، این نتیجه در
S
S
b
e
t
w
e
e
n
=
10
(
99.2
−
101.7
)
2
+
10
(
112.6
−
101.7
)
2
+
10
(
93.3
−
101.7
)
2
=
1956.2
SSbetween = 10 (99.2−101.7) 2 + 10 (112.6−101.7) 2 + 10 (93.3−101.7) )2 = 1956.2
بعد ، برای mmگروه ،
df_{between} = m – 1
بنابراین
برای داده های مثال ما dfbetweendfbetween = 3 – 1 = 2
MSbetween = SSbetweendfbetweenMSbetween = SSbetweendfbetween برای مثال ما ، این خواهد بود
1956.22 = 978.11956.22 = 978.1
اکنون واریانس درون گروه ها رابررسی می کنیم. اول از همه،
SSwithin = Σ (Xi − X¯¯¯¯j) 2 SSwithin = Σ (Xi − X¯j) 2
جایی که
X—j X—میانگین گروه را نشان می دهد؛
XiXi یک مشاهده فردی را نشان می دهد (“نقطه داده”).
برای مثال ما ، داریم
SSwithin = (90−99.2) 2+ (87−99.2) 2 + … + (96−93.3) 2 = 4294.1 SSwithin = (90−99.2) 2+ (87−99.2) 2 + … + (96 93.3 −) 2 = 4294.1
برای nn مشاهدات مستقل و mmگروه های ،
dfwithin = n − mdfwithin = n-m
بنابراین برای مثال ما30-3=27 است
MSwithin = SSwithindfwithinMSwithin = SSwithindfwithin
برای مثال ما ، 159= 1594294.127 = 4294.127
اکنون آماده محاسبه آمار F هستیم:
F = MSbetweenMSwithin F = MSbetweenMSwithin
که منجر به 6.15 = 6.15978.1159 = 978.1159
سرانجام، P = P (F (2،27)> 6.15) = 0.0063P = P (F (2،27)> 6.15) = 0.0063
در صورت تمایل ، اندازه اثر η2 به این صورت محاسبه می شود
Effectsizeη2 = SSbetweenSSbetween + SSwithinEffectsizeη2 = SSbetweenSSbetween + SSwithin
1956.21956.2+4294.1=0.311956.21956.2+429.4=0.31برای مثال ماعبارت است
با تشکر از شما برای خواندن
